Cut Cross Entropy > Torch's version? No.

I just wrote an explainer on CCE and was building a training repo to check CCE convergence on a small LLM. 4 hours after I started working on it, Karpathy released Nanochat!!!

I discuss implementation and results in this short post.

Implementing CCE

Apple has done a great job of making their kernels very easy to integrate and feature-rich.

Karpathy's code has this for calculating loss:

logits = self.lm_head(x)
logits = softcap * torch.tanh(logits / softcap) # logits softcap
logits = logits.float() # use tf32/fp32 for logits
loss = F.cross_entropy(logits.view(-1, logits.size(-1)), targets.view(-1), ignore_index=-1, reduction=loss_reduction)

CCE eliminates self.lm_head(x) which is very memory intensive. Implementing it is simple, we replace all the lines above with:

from cut_cross_entropy import linear_cross_entropy, LinearCrossEntropyImpl
loss = linear_cross_entropy(x, self.lm_head.weight, targets, softcap=softcap, reduction=loss_reduction, ignore_index=-1, impl=LinearCrossEntropyImpl.CCE_KAHAN_FULL)

Results

Now, I have a few variations from base code which could have affected these results. Kahan Sum provides more numerically stable results at a small memory cost. Instead of model_depth = 20, I have model_depth = 10. I only trained over 4k steps and I train base on batch_size = 32 vs CCE with batch_size = 64 (afforded by the lower peak VRAM).

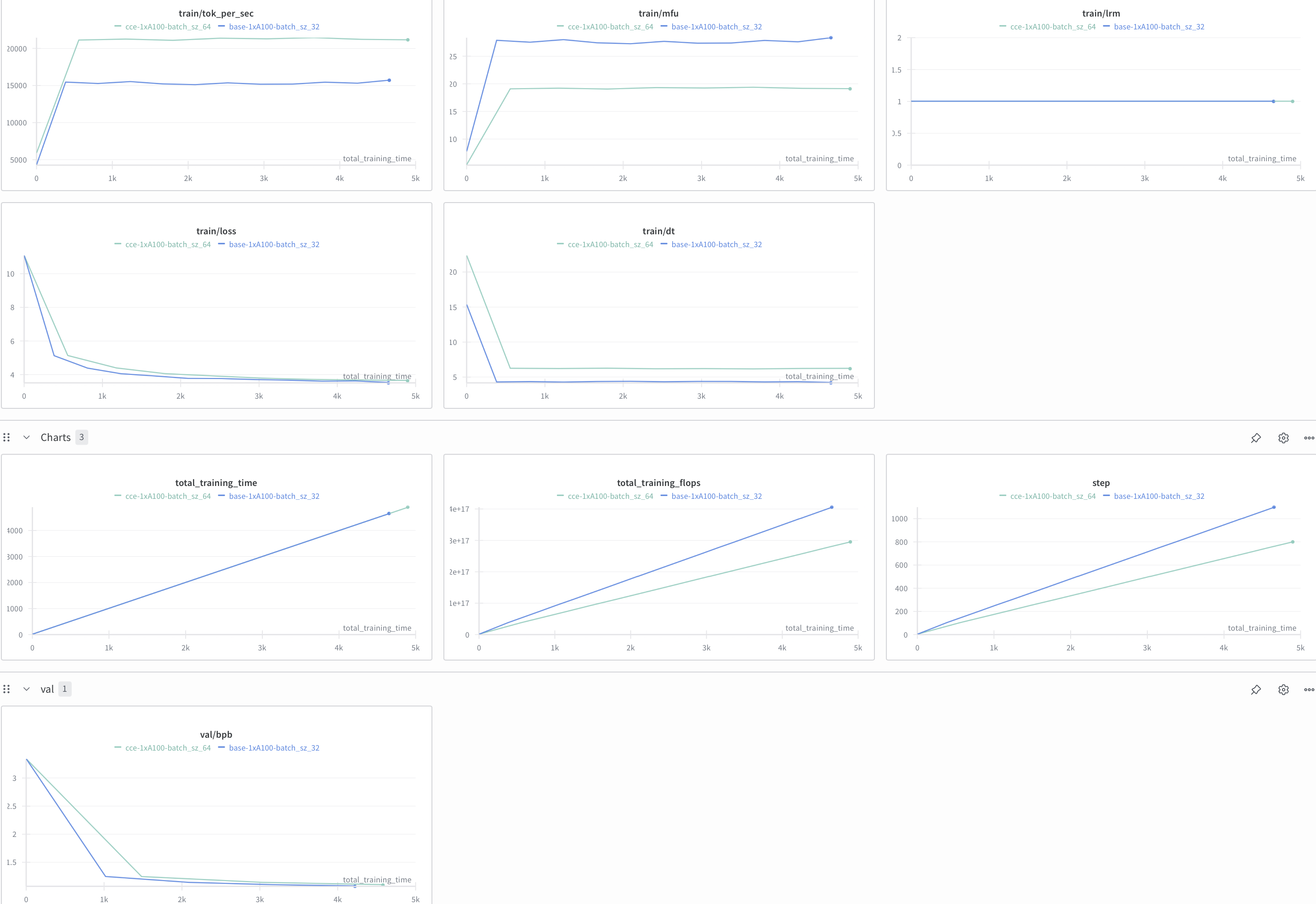
As shown above, Torch's cross entropy gives lower loss than Apple's Cut Cross Entropy. Someone verbally reported the same results to me with Liger's Chunked Cross Entropy. Note, toks/s trained did go up, but loss convergence is preferred over everything!

End Notes

If you have intuition / feedback on this or if you get this working, I'd love to hear it! If I get some time over the next few days, I'll investigate this.

By Omkaar Kamath