Cut Cross Entropy from first principles

If you’ve ever tried training a 70B model and watched your GPU memory bar hit 99%, you’ve already met the enemy: Cross Entropy Loss. It’s silently eating half your VRAM, and Apple’s new Cut Cross Entropy (CCE) paper could help out.

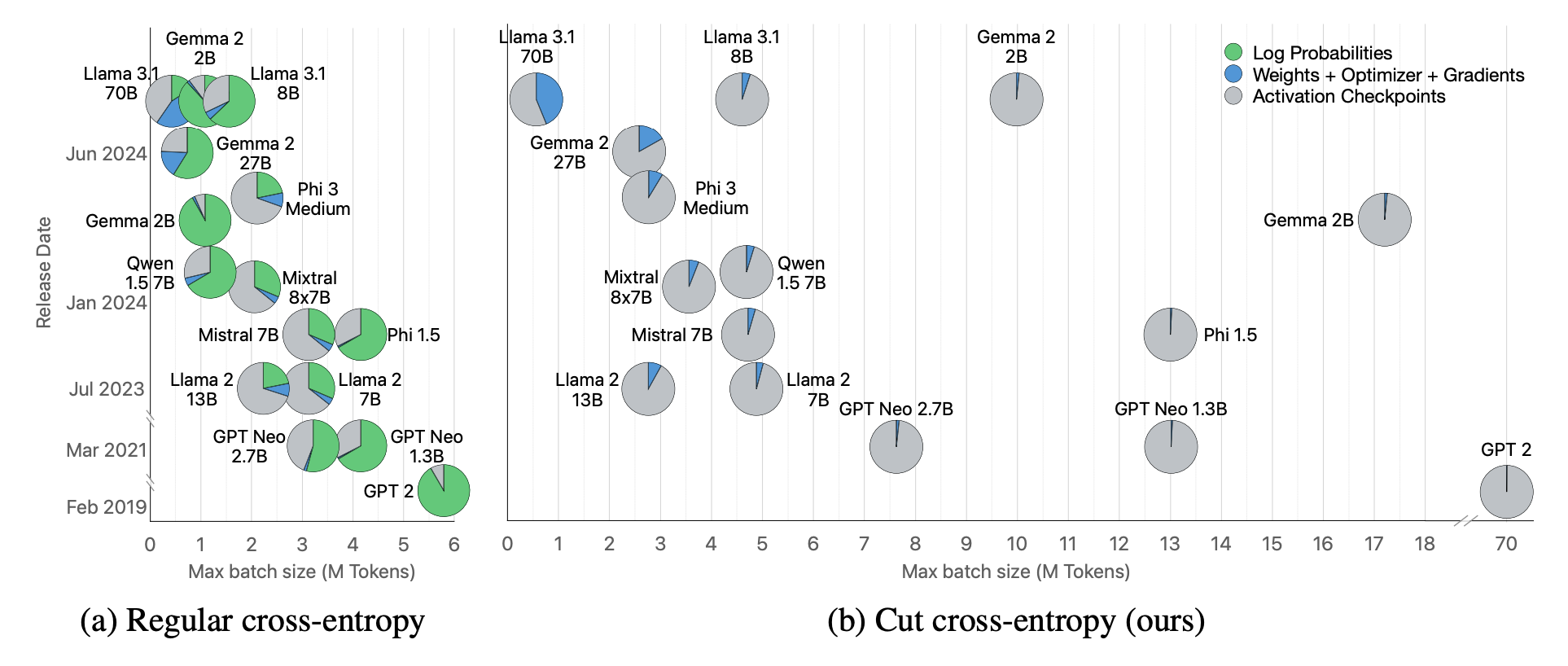
Cross Entropy Loss is commonly calculated by materializing all the logits, which, given the large vocab size and number of batch tokens, leads to exploding VRAM usage. The green pie segment shown in the image below is proportion of memory used by the Cross Entropy loss calculation... notice how with CCE green pie segments seemingly vanish.

Following is an image from Apple's paper showing ratio of memory consumed by different parts of a training run with and without CCE.

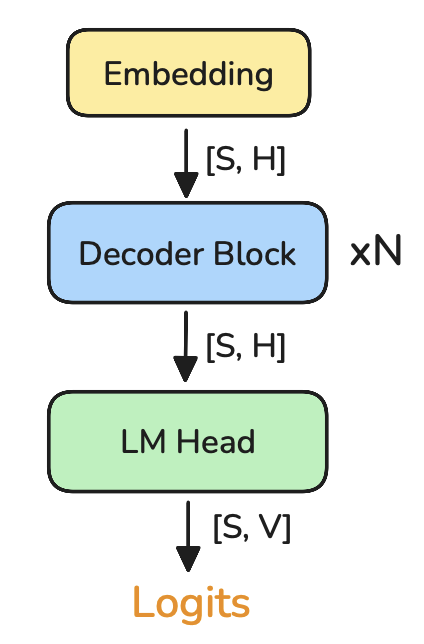
What's up with plain ol' Cross Entropy?

The CE Loss formula = -log(prob(Correct Token))

Probability of a token comes from softmax over the vocab dimension of the logits tensor.

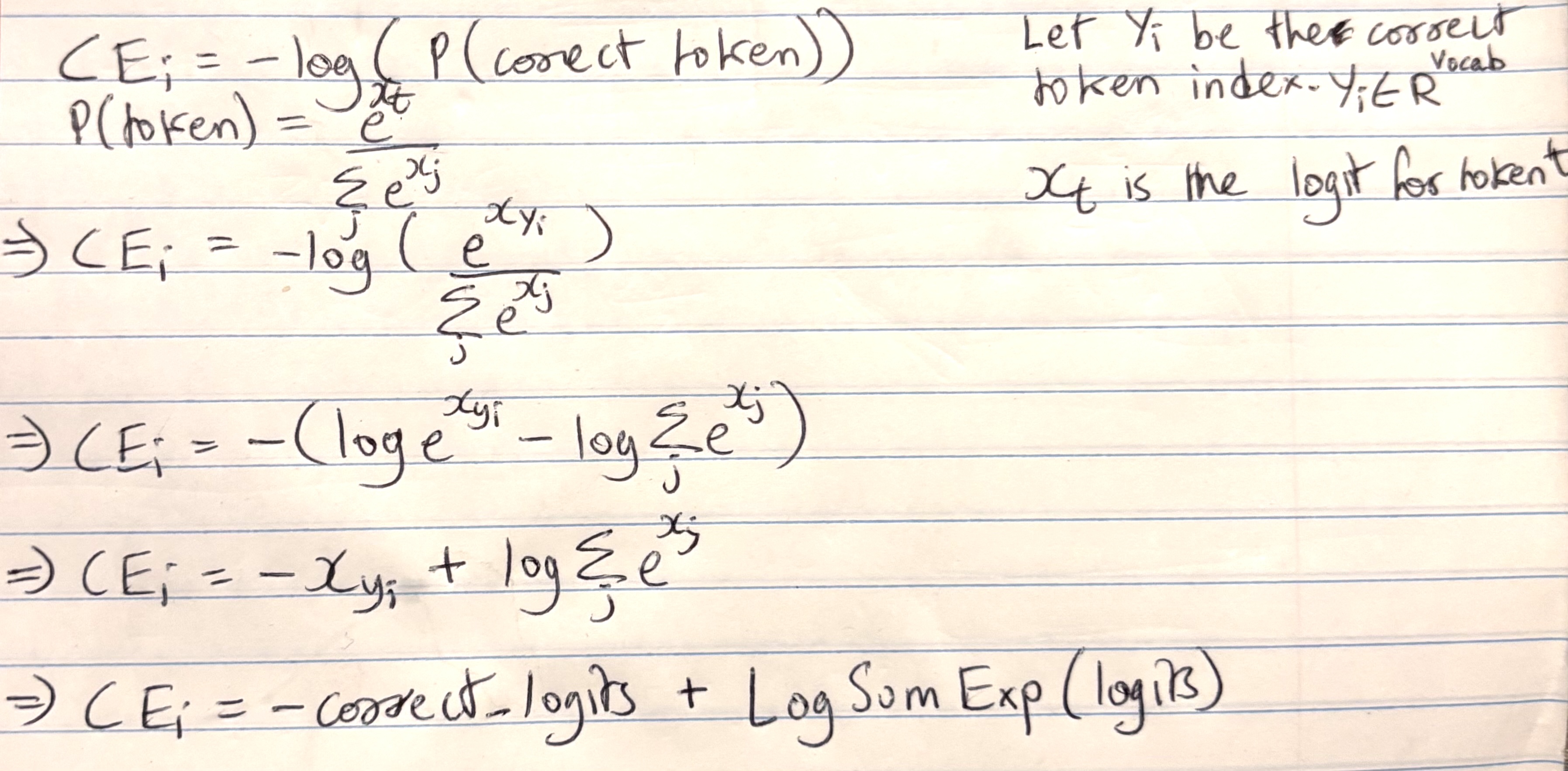
Putting all this together and a few math tricks, we get loss = -correct_token + LSE

The most naive form of Cross Entropy loss calculation would be:

logits = E @ C.T # <- Total size of tensor: Seq Len * Vocab Size * 4
probs = softmax(logits, dim=-1)  # <- Total size of tensor: Seq Len * Vocab Size * 4
loss = -log(probs[:, target_tokens])

That would need too much memory, but thankfully, we already do something better. We refactor the formula with some maths (worked out below). Right now, CE loss is calculated as follows:

logits = E @ C.T # <- Total size of tensor: Seq Len * Vocab Size * 4
LSE = torch.logsumexp(logits, dim=-1) # <- Total size of tensor: Seq Len * 4
target_logits = logits[:, target_tokens] # <- Total size of tensor: Seq Len * 4
loss = -target_logits + LSE

The problem here is that we still waste a lot of memory materializing the logits. Training on larger sequence lengths, batch sizes, and vocabulary sizes results in a memory explosion.

To give you an idea of the wastage, let's imagine you are training a Llama 70B (vocab_size = 128,256) with batch_size = 128 (assume no grad accum) and sequence length = 8,192. The logits size in bytes would be (128,256 x 128 x 8192 x 4) = 501GB to store FP32 logits... Half a terabyte for one forward pass. It’s such a big waste that I suspect large labs have already solved this internally.

Cut Cross Entropy

The question is how to calculate log(LSE) without materializing the full logit table. Simple: split the work into SRAM-sized chunks and compute only the LogSumExp's on the fly. DSLs like Triton are purpose-built for writing efficient kernels based on this principle.

To calculate loss = -target_logits + log_sum_exp without materializing full logits, we need two kernels: Indexed Matmul which calculates target_logits = hidden @ lm_head[target_ids] and LogSumExp log_sum_exp = log(∑exp(hidden @ lm_head))

You can check out my triton implementations for the forward kernels here: IndexedMatmul and LogSumExp. Below is the performance compared to vanilla PyTorch (torch compile roughly the same perf. as vanilla PyTorch.)

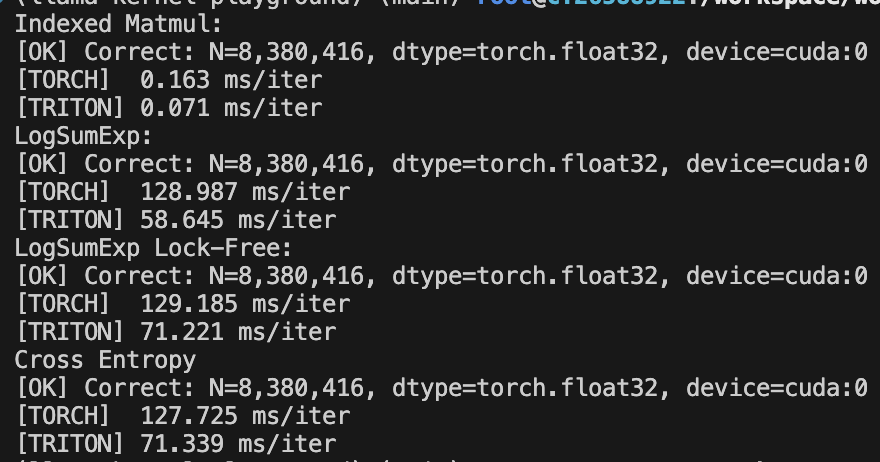
While the forward kernels are much faster and more memory-efficient, their solution is simple. What happens to the backward pass?

Backward Pass

So far, we’ve handled forward passes, but training means we also need gradients. Is that possible without the full logits? ofc.

This is my handwritten derivation for the backward pass and the derivative of the loss with respect to activations and the LM head.

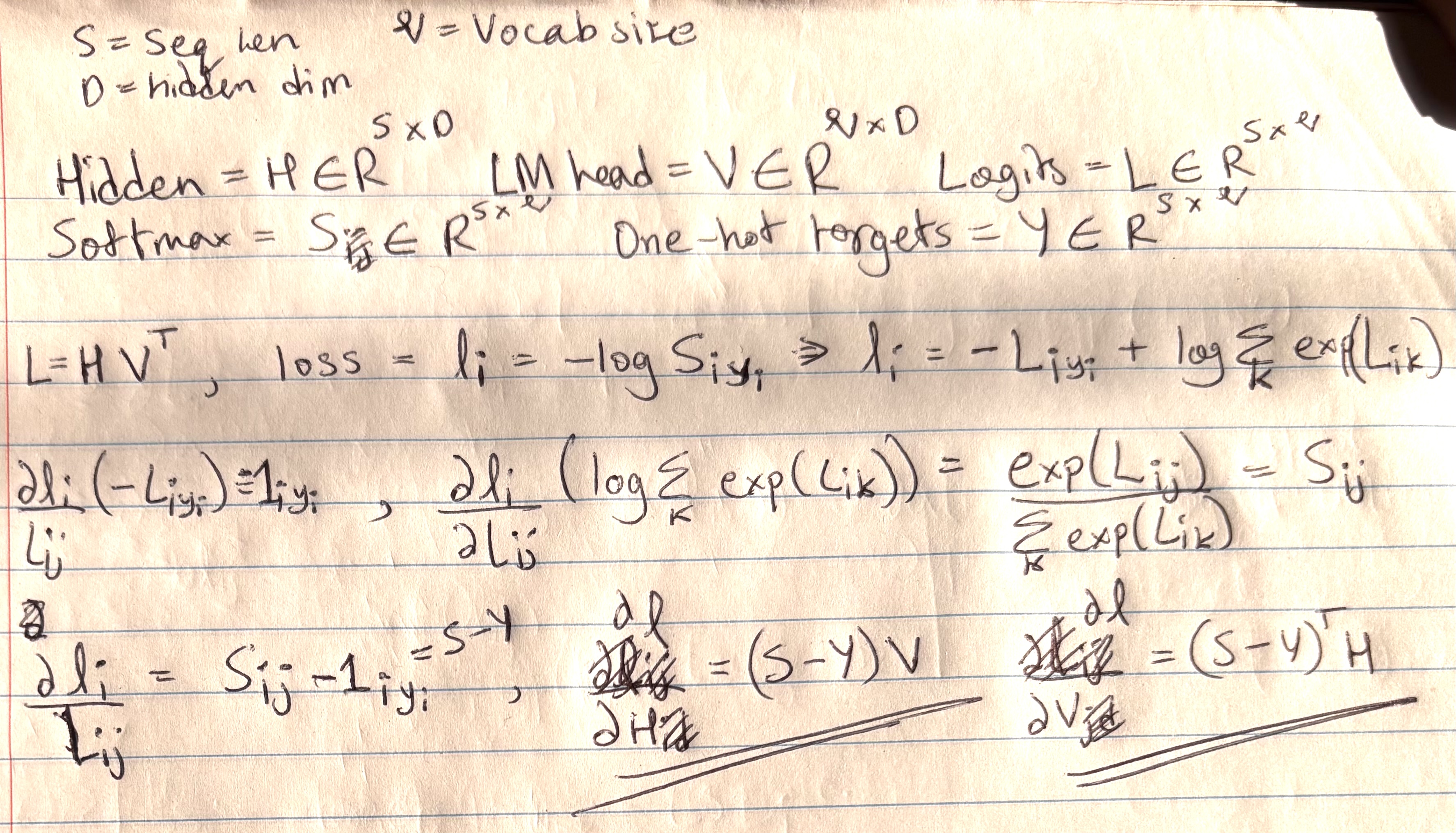
Good blog for math behind derivative of LogSumExp being Softmax.

Backward passes are a bit more complicated in general. Apple used some smart tricks to compute them faster such as:

• LSE Re-use: Instead of calculating softmax from scratch, they use the already materialized LSE (shown in backward pass algorithm below). softmax = exp(logit - LSE)
• Gradient Filtering: Any softmax value along the vocab dim less than pre-set ɛ will be ignored in gradient calculation. In practice (triton), we work on blocks of softmax values at a time, so we check if max(values) < ɛ and if it is, set gradient of the blocks as 0. Has no effect on accuracy given ɛ is small (e.g. 10^-12). Funnily, this means only 0.02% of gradients need to be calculated in practice (stated by CCE paper).
• Vocabulary Sorting: This complements gradient filtering. Wouldn't it be great if the most common vocabs are stacked at the start of the matrix? This will significantly increase blocks with softmax values < ɛ and would result in less gradient blocks needing calculation.

Here is my simplified backward kernel similar to the algorithm shown above from Apple's paper. While I didn’t implement vocabulary sorting, simply adding coarse gradient filtering improved performance from 18% to 250% of PyTorch’s speed!!!

Note: These are not production-level kernels, I wanted to write a simpler working but fast kernel for illustration at the expense of other features. I don't like the numerical precision level I have, if I had more time, I'd try Kahan summation like in Apple's code.

End notes

We reduced memory usage along with forward AND backward computation time. Wins like this are rare. Companies offering finetuning services like Unsloth benefit a lot as they can now cut costs related to compute. This was a fun exploration, I love writing Triton.

By Omkaar Kamath