Decisive guide on Speculative Decoding

Recently, I've found myself looking into multi-batch inference frameworks like vLLM and techniques to infer on models faster. Some techniques require tweaking the architecture and others are systems.

One such technique is speculative decoding (SD). I wanted to explore this further and share an implementation.

What is speculative decoding (SD)?

The idea is to somehow (more on this below) make educated guesses on the next k tokens and then, verify these guesses with a big model. Why does this work and what does "verification" mean in this context? I'll cover that later.

While I have not read all the literature in this field, I (with the help of deep research) have identified a few main themes which I explain in this blog.

This paper (Leviathan et al.) gave birth to SD and our first method works off it ->

Draft-And-Verify approach

The draft model is a smaller version of the target model that we want to run inference on. Ex. Llama3-3b can be the draft model for Llama3-70b. The idea is simple, draft model generates n tokens. We feed the n tokens into target model which produces logits for previous tokens + one output 1 token. With simple checks against draft's vs target's logits produced, we accept or reject the produced tokens.

The caveat here is, during generation, speculative decoded output distribution is same as the target model's output distribution.

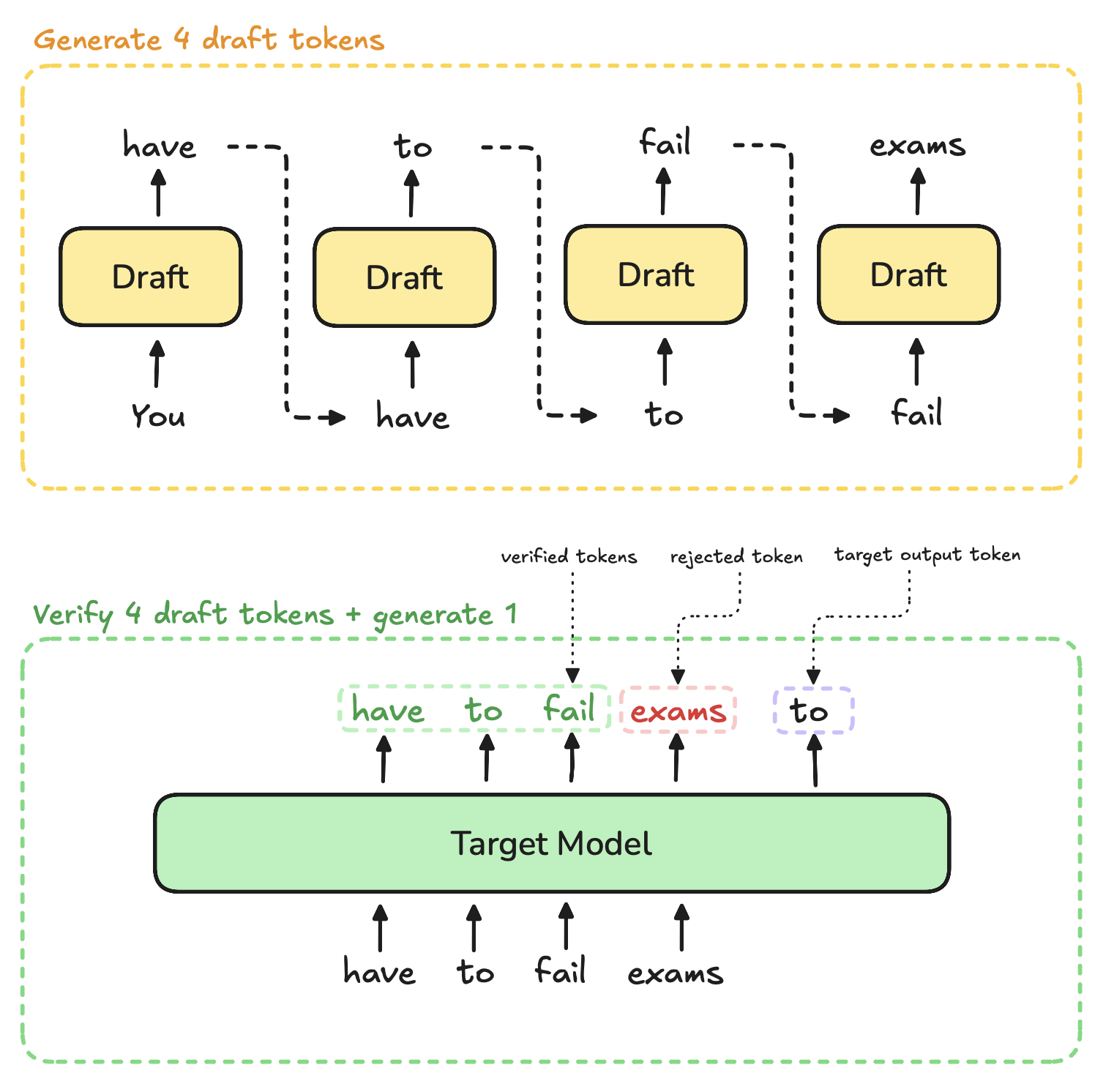
For demonstration, I implemented Qwen2-1.5B as target and Qwen2-0.5B as the draft.

I recommend reading my implementation code (feel free to disregard my Qwen2 class). This is the pseudocode for the process:

while num_tokens_generated < num_tokens_to_generate:
    k_to_draft = 4
    draft_tokens, draft_logits = draft_model(curr_tokens, n=k_to_draft)
    target_token, target_logits = target_model(curr_tokens + draft_tokens, n=1)

    let `accepted_tokens` be an empty list
    let `next_token` be an empty list

    for each draft_token:
        let `q_logits` be corresponding draft_logits to draft_token
        let `p_logits` be corresponding target_logits to draft_token

        let `qx` be corresponding softmax'd logit value to draft_token from q_logits
        let `px` be corresponding softmax'd logit value to draft_token from p_logits

        if qx <= px then
            Add token to `accepted_tokens`
        else then
            if random_float() < px/qx then
                Add token to `accepted_tokens`
            else then
                # reject any more samples
                residual = norm(max(p_logits - q_logits, 0))
                new_token = multinomial_sample(residual)
                break
    
    if len(accepted_tokens) = k_to_draft then
        new_token = target_token
    
    curr_tokens = new_token

I omitted cursor logic which makes sure we don't have to run prefill on the whole set of tokens everytime.

Simple KVCache optimization runs at 29 tok/s while draft-and-verify (with KVCache) runs at 20 tok/s (on my M4 Mac Book Air). This likely happens because the size difference is not monumental and the overhead involved in running two models make spec decode slower. Speedup depends on how many draft tokens are accepted on average and the compute cost ratio between draft and target models.

While I laid out a basic version, there are many papers building on top of this core idea. Other ideas include using a tiny distilled model, etc.

N-gram approach

N-gram is a simple approach which builds a mapping of n-gram -> n-following-tokens. Whenever the last n generated tokens are in the mapping, you speculate the n-following tokens.

This image from vLLM's blog illustrates it perfectly.

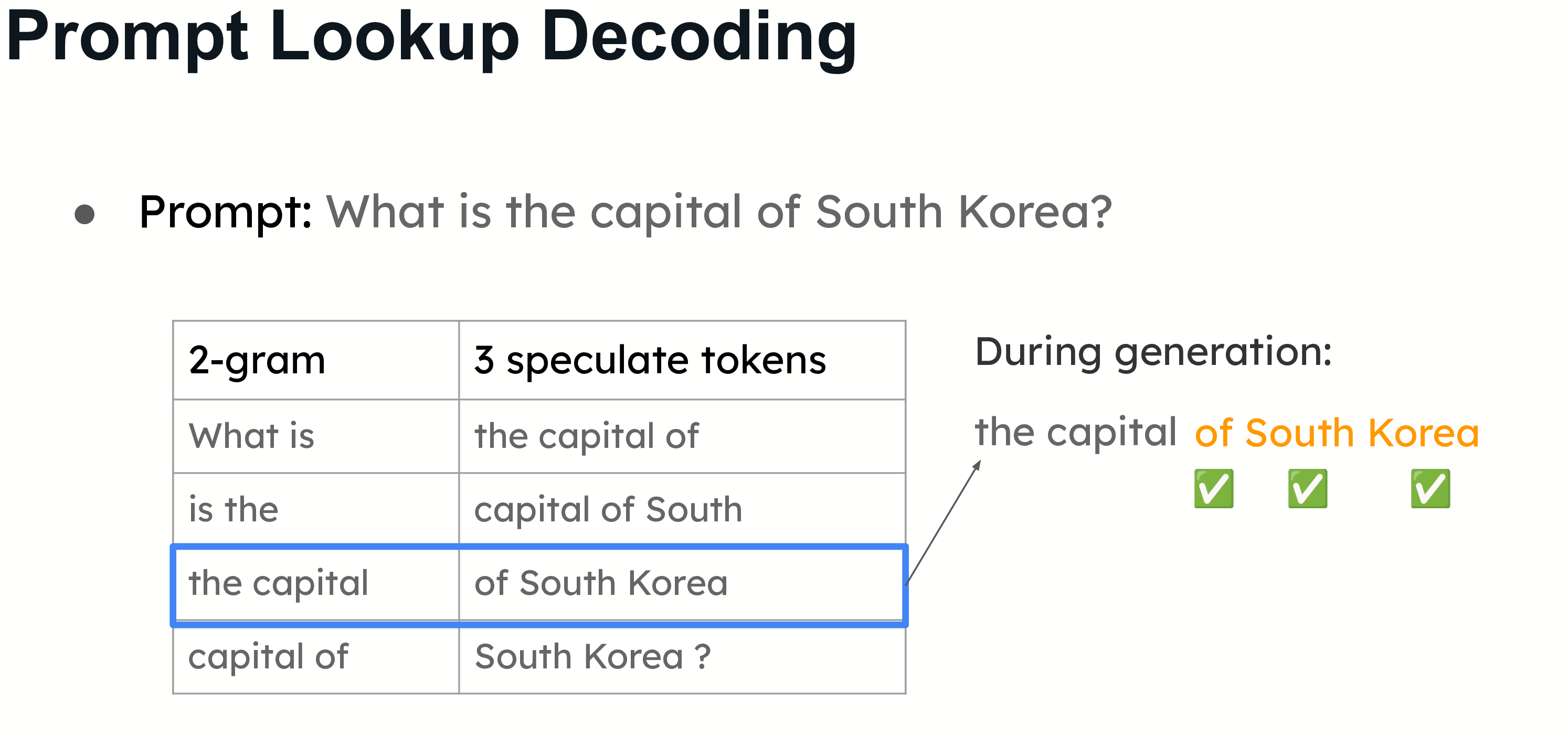
As you might point out, this only works well when there are specific repeated n-grams across prompt + generation which may not be the case in all types of use cases.

Auxiliary Heads approach

The Medusa paper describes adding k decoding heads which take the last hidden state's output as their inputs and output the hidden representation for the k+1 token. The diagram below should make it clear.

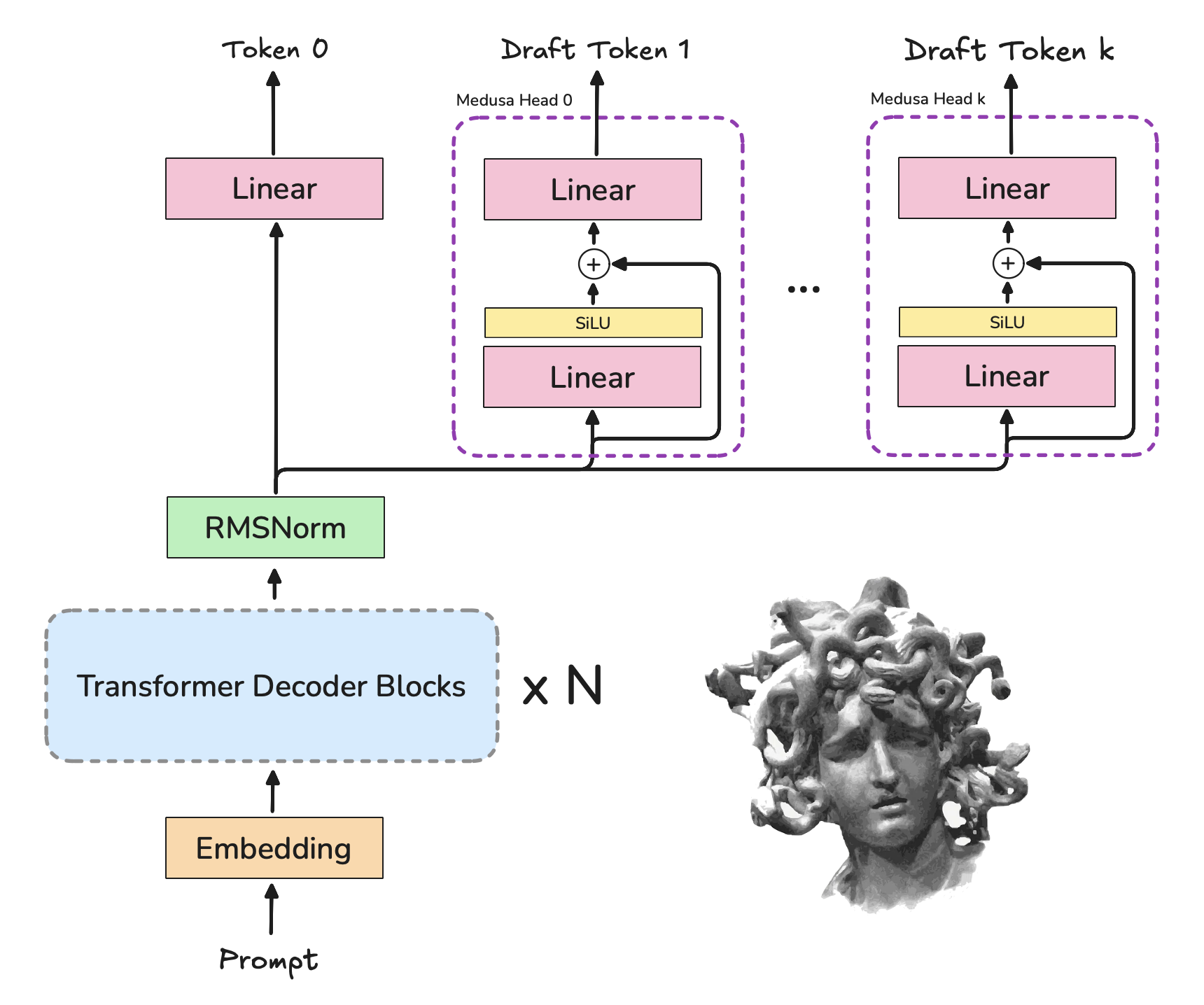
Feature Re-use approach

Eagle-3 is a relatively new paper (builds on top of EAGLE and EAGLE-2). I like their intuition... EAGLE-3 drops feature regression (predicting next token's features through regression) and does direct token prediction using a fused low/mid/high layer feature vector from the target. They report a 6.5× total speedup in their benchmarks. The following illustration is from the paper linked above.

The draft model has to be pretrained jointly with frozen target model. Predicting a new draft token simply needs a re-run of the draft model with all the previous predicted draft tokens.

Conclusion

Speculative decoding pays off when there is a big draft–target gap (1B + 70B), the target model is expensive AND draft is close enough in quality that acceptance (verification) rate is high.

As an aside, this is Google AI search's results with and without speculative decoding:

This video and the video in the introduction are both from Google's blog.

Sources

• vLLM's Blog on Speculative Decoding
• Aleksa's Blog on vLLM